Online Fragen - Gültige Praxis zu Ihrer Databricks-Certified-Professional-Data-Scientist Prüfung (Aktualisierte 140 Fragen) [Q15-Q30]

NR. 15 Angenommen, wir interessieren uns für die Faktoren, die beeinflussen, ob ein politischer Kandidat eine Wahl gewinnt. Die Ergebnisvariable (Antwortvariable) ist binär (0/1): gewinnen oder verlieren. Die interessierenden Vorhersagevariablen sind der für den Wahlkampf ausgegebene Geldbetrag, die für den Wahlkampf aufgewendete Zeit und die Tatsache, ob der Kandidat ein Amtsinhaber ist oder nicht.
Oben ist ein Beispiel für

NR. 16 Welcher Vektor weist bei der Projektion eines mehrdimensionalen Datensatzes die größte Varianz auf?

NR. 17 Sie arbeiten an einem Problem, bei dem Sie vorhersagen müssen, ob der Antrag gültig ist oder nicht. Dabei stellen Sie fest, dass die meisten Anträge mit Rechtschreibfehlern und Korrekturen in den manuell ausgefüllten Antragsformularen mit ehrlichen Anträgen verglichen werden. Welche der folgenden Techniken ist geeignet, um herauszufinden, ob der Antrag gültig ist oder nicht?

NR. 18 Sie haben k-means clustering verwendet, um das Verhalten von 100.000 Kunden eines Einzelhandelsgeschäfts zu klassifizieren. Sie entscheiden sich, Haushaltseinkommen, Alter, Geschlecht und jährliche Kaufsumme als Maßzahlen zu verwenden. Sie haben sich für die Verwendung von 8 Clustern entschieden und stellen fest, dass 2 Clustern nur 3 Kunden zugeordnet sind. Was sollten Sie tun?

NR. 19 Siehe Beilage

In der Abbildung stellt die x-Achse die abgeleitete Wahrscheinlichkeit dar, dass ein Kreditnehmer mit einem Kredit in Verzug gerät. Die rosa Farbe steht für Kreditnehmer, von denen bekannt ist, dass sie ihren Kredit nicht zurückzahlen, und die blaue Farbe für Kreditnehmer, von denen bekannt ist, dass sie ihren Kredit zurückzahlen. Mit welcher Analysemethode lassen sich die Wahrscheinlichkeiten ermitteln, die zur Erstellung dieses Schaubilds benötigt werden?

NR. 20 Welche der folgenden Verteilungen ist eine kontinuierliche Wahrscheinlichkeitsverteilung?

NR. 21 Sie haben die Daten von 1000 Patienten mit der Größe und dem Alter. Das Alter in Jahren und die Größe in Metern. Sie wollten anhand dieser beiden Attribute ein Cluster erstellen. Bei der Erstellung des Clusters sollte die Wirkung von Alter und Größe nahezu gleich sein. Was können Sie tun?

NR. 22 Welche der folgenden Aussagen zum linearen Regressionsmodell trifft zu?

NR. 23 Welche der folgenden Angaben beschreiben die Hauptkomponentenanalyse am besten

NR. 24 Angenommen, Sie haben ein Modell für ein Bewertungssystem erstellt, das zwischen 1 und 5 Sternen bewertet. Und Sie haben berechnet, dass der RMSE-Wert 1,0 beträgt.

NR. 25 Ihr Kunde hat Ihnen 2. 000 unbeschriftete Datensätze in drei Gruppen zur Verfügung gestellt. Welches ist die richtige Analysemethode, die Sie anwenden sollten?

NR. 26 Wählen Sie die Option, bei der die Regressionsalgorithmen nicht am besten geeignet sind

NR. 27 In welcher Phase des Lebenszyklus werden Test- und Trainingsdatensätze erstellt?

NR. 28 Szenario: Angenommen, Bob kann sich entscheiden, mit einem von drei Verkehrsmitteln zur Arbeit zu fahren: mit dem Auto, dem Bus oder dem Nahverkehrszug. Wenn er sich für das Auto entscheidet, besteht aufgrund des hohen Verkehrsaufkommens eine Wahrscheinlichkeit von 50%, dass er zu spät kommt. Wenn er mit dem Bus fährt, der über spezielle reservierte Fahrspuren verfügt, aber manchmal überfüllt ist, beträgt die Wahrscheinlichkeit einer Verspätung nur 20%. Die S-Bahn ist mit einer Wahrscheinlichkeit von nur 1 % fast nie verspätet, ist aber teurer als der Bus.
Angenommen, Bob kommt eines Tages zu spät, und sein Chef möchte die Wahrscheinlichkeit schätzen, dass er an diesem Tag mit dem Auto zur Arbeit gefahren ist. Da er nicht weiß, welches Verkehrsmittel Bob normalerweise benutzt, gibt er eine vorherige Wahrscheinlichkeit von
1 3 zu jeder der drei Möglichkeiten. Welche der folgenden Methoden wird der Chef anwenden, um die Wahrscheinlichkeit zu schätzen, dass Bob zur Arbeit gefahren ist?

NR. 29 Welches der folgenden Beispiele ist ein korrektes Beispiel für die Zielvariable bei der Regression (überwachtes Lernen)?

NR. 30 Angenommen, es soll die Wahrscheinlichkeit berechnet werden, dass ein Fußgänger von einem Auto überfahren wird, während er an einem Fußgängerüberweg die Kröte überquert, ohne auf die Ampel zu achten. Sei H eine diskrete Zufallsvariable, die einen Wert aus (getroffen. nicht getroffen) annimmt. Sei L eine diskrete Zufallsvariable, die einen Wert aus (Rot. Gelb.
Grün).
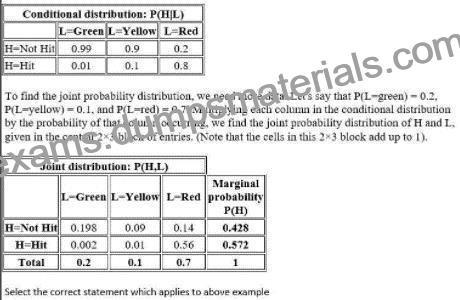
Realistischerweise ist H von L abhängig, d. h. P(H = getroffen) und P(H = nicht getroffen) nehmen unterschiedliche Werte an, je nachdem ob L rot, gelb oder grün ist. Es ist zum Beispiel sehr viel wahrscheinlicher, dass eine Person von einem Auto angefahren wird, wenn sie versucht, die Straße zu überqueren, während die Ampel für den Querverkehr grün ist, als wenn sie rot ist. Mit anderen Worten, für jedes mögliche Wertepaar für die Hand L. muss man also die gemeinsame Wahrscheinlichkeitsverteilung von H und L betrachten, um die Wahrscheinlichkeit* zu ermitteln, dass dieses Paar von Ereignissen zusammen auftritt, wenn der Fußgänger den Zustand der Ampel ignoriert Die folgende Tabelle zeigt die bedingten Wahrscheinlichkeiten, gebissen zu werden. abhängig vom Zustand der Ampel (Beachten Sie, dass die Spalten in dieser Tabelle 1 ergeben müssen, da die Wahrscheinlichkeit, getroffen oder nicht getroffen zu werden, unabhängig vom Zustand der Ampel 1 ist).